Data description
We create the variable trans with some minor modification in order to set easier to remember column names, and set the Donation as a factor.
So the labels are:
- Recency: months since last donation
- Frequency: total number of donation
- Monetary: total blood donated in c.c.
- TFirst: months since first donation
- Donation: If the donor return in march
Descriptive Stats
First a summary of the data is calculated. Is possible to realize that the average of time since the last donation is 9 months. And have a mean of 5 donations. They give a liter of blood. And its been a mean of 2 year and 9 months since the firs donation.nd just 178 subjects return in march.
summary(trans)
## Recency Frequency Monetary TFirst Donation ## Min. : 0.000 Min. : 1.000 Min. : 250 Min. : 2.00 NonDonate:570 ## 1st Qu.: 2.750 1st Qu.: 2.000 1st Qu.: 500 1st Qu.:16.00 Donate :178 ## Median : 7.000 Median : 4.000 Median : 1000 Median :28.00 ## Mean : 9.507 Mean : 5.515 Mean : 1379 Mean :34.28 ## 3rd Qu.:14.000 3rd Qu.: 7.000 3rd Qu.: 1750 3rd Qu.:50.00 ## Max. :74.000 Max. :50.000 Max. :12500 Max. :98.00
Boxplots
boxplot(trans)

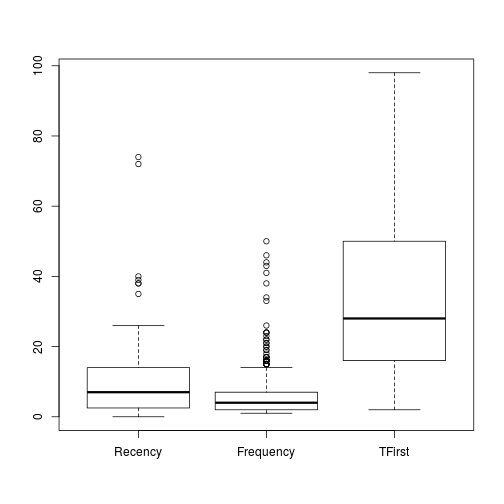
Because the Donation is a factor of the dependent variable, the creation of their boxplot can be avoided. And the M boxplot is out of range from the rest so we can create a extra boxplot.
boxplot(trans[c(-3,-5)])
boxplot(trans$Monetary, xlab = c("Monetary"), ylab = "c.c.")

Histograms
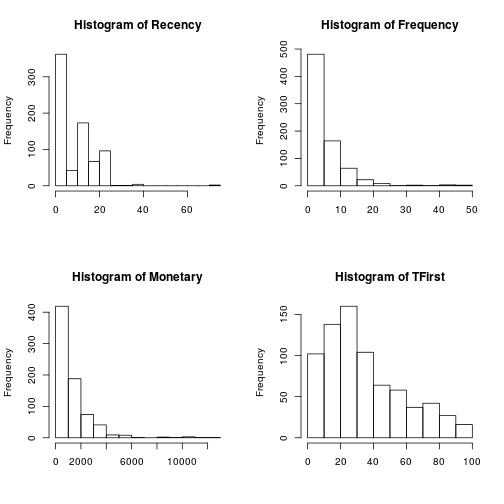
Standard count histograms were created in order to look at the distribution of the measurements, Recency, Frequency, Monetary and First Time Donation. For Donation and with two values, is not necessary an histogram.
par(mfrow = c(2, 2)) for (i in 1:length(trans[1:4])) { hist(trans[, i], main = paste("Histogram of", names(trans)[i]), xlab = NA) }
Density plot
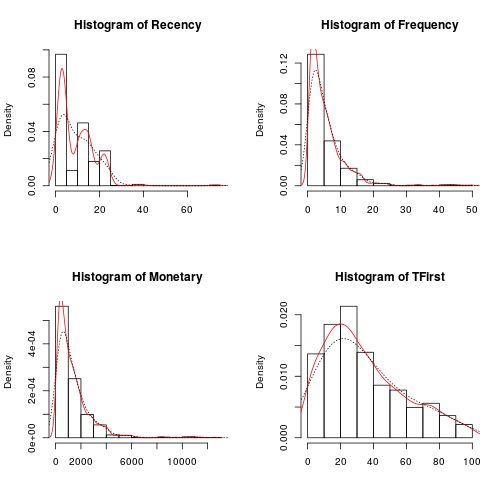
Then the Probability histograms, which shows the probability of distribution for each variable are overlapped whit two Density plots, in red the density plot for the accumulation of values, and the dotted line shows the adjusted density plot.
par(mfrow = c(2, 2)) for (i in 1:length(trans[1:4])) { hist(trans[, i], main = paste("Histogram of", names(trans)[i]), xlab = NA, prob = T) lines(density(trans[, i]), col = "red") lines(density(trans[, i], adjust = 2), lty = "dotted") }
Classification Tree
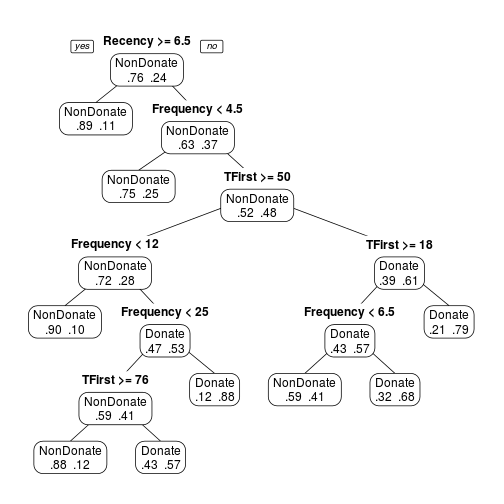
First a Classification Tree with a formula which combine Dependent Variables in function of Independent Variables.
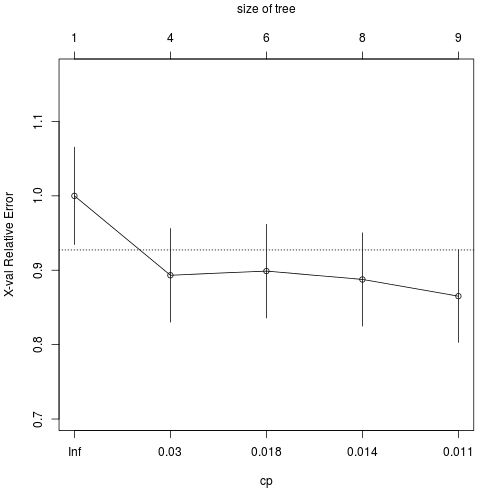
Note: From this tree is possible to acquire the complexity values(CP) which are going to be used in the Prune function.
transtree <- rpart(Donation ~ Recency + Frequency + Monetary + TFirst, method = "class", data = trans) prp(transtree)

printcp(transtree)
## ## Classification tree: ## rpart(formula = Donation ~ Recency + Frequency + Monetary + TFirst, ## data = trans, method = "class") ## ## Variables actually used in tree construction: ## [1] Frequency Recency TFirst ## ## Root node error: 178/748 = 0.23797 ## ## n= 748 ## ## CP nsplit rel error xerror xstd ## 1 0.046816 0 1.00000 1.00000 0.065430 ## 2 0.019663 3 0.85955 0.89326 0.062862 ## 3 0.016854 5 0.82022 0.89888 0.063005 ## 4 0.011236 7 0.78652 0.88764 0.062717 ## 5 0.010000 8 0.77528 0.86517 0.062127
plotcp(transtree)
Pruning
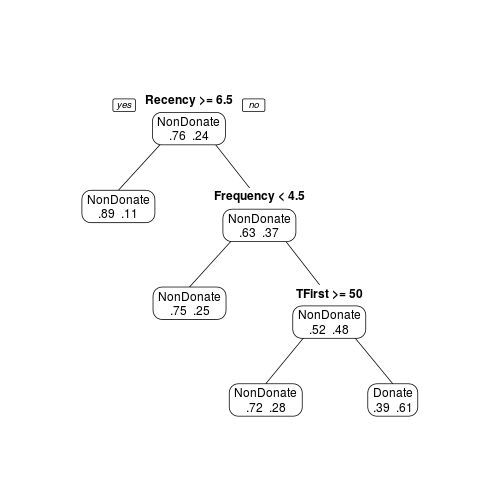
With the CP we can prune the tree in order to get the optimal number of nodes with the minor Relative Error.
transtree.pruned <- prune(transtree, cp = 0.011) prp(transtree.pruned, type = 1, extra = 4, varlen = 0)
Another option is to use the smallest tree whose cross-validation error is within one standard error of the smaller. In this case could be cp = 0.03, easy to see in the plotcp.
transtree.pruned <- prune(transtree, cp = 0.03) prp(transtree.pruned, type = 1, extra = 4, varlen = 0)
Random Forest
The Random Forest approach use a series of random generate Trees in order to get the variables which better explain the dependent data.
set.seed(778688) transforest <- randomForest(Donation ~ Recency + Frequency + Monetary + TFirst, data = trans, importance = T) transforest
## ## Call: ## randomForest(formula = Donation ~ Recency + Frequency + Monetary + TFirst, data = trans, importance = T) ## Type of random forest: classification ## Number of trees: 500 ## No. of variables tried at each split: 2 ## ## OOB estimate of error rate: 24.73% ## Confusion matrix: ## NonDonate Donate class.error ## NonDonate 510 60 0.1052632 ## Donate 125 53 0.7022472
Importance table represents how much removing each variable reduces the accuracy of the model. And the Right (MeanDecreaseGini) shows how each variable reduces impurity at all tree nodes.
importance(transforest)
## NonDonate Donate MeanDecreaseAccuracy MeanDecreaseGini ## Recency 10.24412 32.022719 24.92773 53.62862 ## Frequency 18.35183 7.706997 23.16787 31.22092 ## Monetary 17.67934 6.341006 21.80268 30.97825 ## TFirst 18.23311 2.851695 20.05375 74.34059
varImpPlot(transforest, main = NA)

Review of Questions
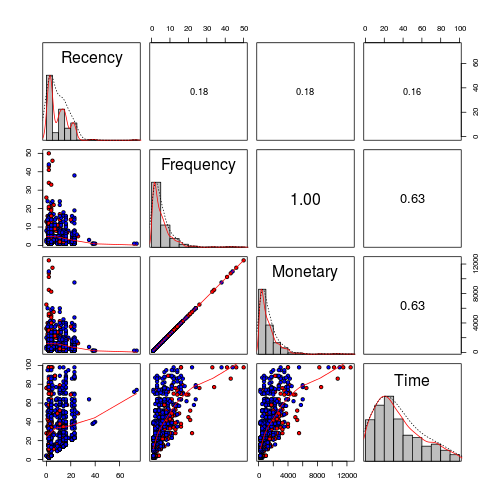
Actually when the correlation is reviwed between Monetary and Frequency, the correlations is 1.
cor.test(trans$Monetary, trans$Frequency)
## ## Pearson's product-moment correlation ## ## data: trans$Monetary and trans$Frequency ## t = 1296100000, df = 746, p-value < 2.2e-16 ## alternative hypothesis: true correlation is not equal to 0 ## 95 percent confidence interval: ## 1 1 ## sample estimates: ## cor ## 1
And there is a high correlation between Monetary and Frecuency with the time from the first donation variable (TFirst)
cor(trans[-5])
## Recency Frequency Monetary TFirst ## Recency 1.0000000 -0.1827455 -0.1827455 0.1606181 ## Frequency -0.1827455 1.0000000 1.0000000 0.6349403 ## Monetary -0.1827455 1.0000000 1.0000000 0.6349403 ## TFirst 0.1606181 0.6349403 0.6349403 1.0000000
It is important to notice that the correlation is not only between these two variables, but also the tendecy of Time with the same two(Frequency and Monetary). Youn can see the donators(red), non donator(red).
x <- pairs(dat[-5], cex = 1,pch=21, bg=c("blue","red")[dat$Donates], lower.panel = panel.smooth, diag.panel = panel.hist, upper.panel = panel.cor)
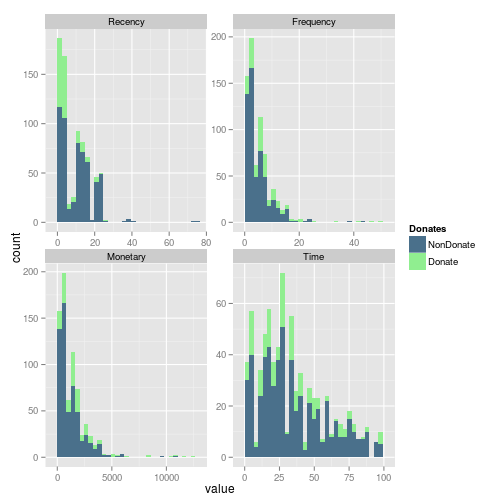
Wen we include in the histograms the information of donation, we can easily see that in the Frequecy, the most of the frequent donators, donates. And looks like an important number of donators come recently donates.
gg <- ggplot(m.dat,aes(x=value, fill=Donates)) + geom_histogram() + scale_fill_manual(values=c("NonDonate"="skyblue4","Donate"="lightgreen")) + facet_wrap(~variable, scales ="free") print(gg)
In fact whe we review the fill representation of each condition, the Frequency looks like a good variable to explore. Mainly beacause of the subjects which more frequently donates return to donates.
gg<- ggplot(m.dat,aes(x=value, fill=Donates)) + geom_histogram(position="fill") + scale_fill_manual(values=c("NonDonate"="skyblue4","Donate"="lightgreen")) + facet_wrap(~variable, scales ="free") print(gg)
